Genetic programming

There are many concepts and algorithms commonly used in artificial intelligence that are inspired by the real world’s phenomena, especially when it comes to biology. Genetic programming is part of a huge family of evolutionary algorithms and before we get to it, let us summarize the basics of evolutionary algorithms. Their main purpose is to find an optimal solution to all kinds of problems, including mathematical ones, which they try to approximate. Such algorithms are generally called heuristic in opposition to deterministic ones, which are designed to find the exact or exactly the best solution to a given problem. There are two main issues with deterministic algorithms. The first one is that it is almost impossible to apply them on constantly changing real-time analyses or chaotic systems. The second issue is that their time complexity, especially with non-deterministic tasks, is usually exponential, while the heuristic algorithms are approximately quadratic.

Evolutionary algorithms are inspired by biological evolution and the way they approximate the optimal solution is thus based on finding an individual solution with the highest fitness in the environment given by the task assignment. First, the programmer must define the size of the initial population, that is the number of the individuals represented by objects (representation of individual solutions, so one individual can be a series of numbers etc.), and create such individuals randomly or using some initial guessing or even outputs of other algorithms. Next is the actual iteration of the algorithms through usually fixed number of generations, or some other termination, which will break the iteration when a certain generation represented by the population or by some best-fit individual is found to represent the optimal solution to the given task. Every generation, every iteration is based on the output from the previous one.

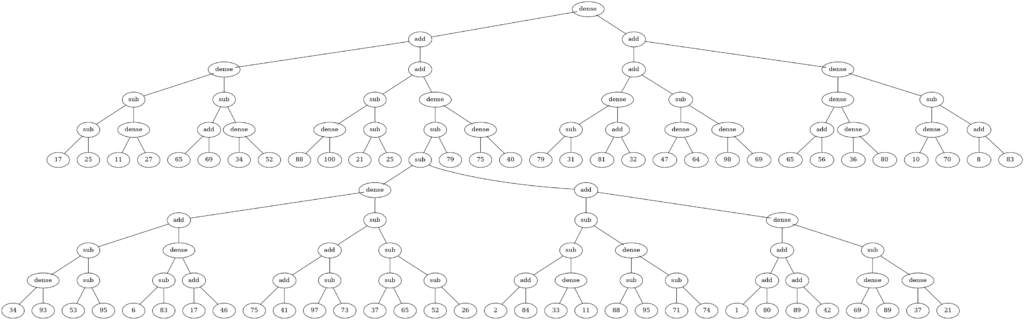Example of a simple program represented by a tree, built by genetic programming.

As the first step during the iteration, every individual inside the population is evaluated/tested if it represents the optimal solution and based on that its fitness is calculated, usually represented by a number. Only those individuals that have the highest (or the lowest, based on the nature of the task) fitness will be selected for reproduction. How many of the individuals there will be in the reproduction is given by a parameter specifically guessed for the given task. From the selected individuals, the algorithm then creates new individuals as offsprings based on the data from the parent individuals. It is usually done in two ways: crossover of the parents and a random mutation. If each parent is represented by a series of data, one point crossover would simply create two new individuals by joining the data from the first parent to a certain point in the series with the data from the given point on from the series of the second individual. Then, each offspring will be mutated, usually one or just a few numbers would be randomly modified. Mutation helps to avoid locally optimal solutions, that is the ones that seem optimal only from the perspective of the nearest possible solutions. The new generation is based on some of the offsprings and some of the individuals from the previous generation, again based on an input parameter.

Genetic programming uses this general approach, but its focus is not on solving mathematical assignments, but creating programs themselves by using other programs or pieces of code such as functions. Imagine an object representing a car. It has the following methods: go forward, turn left, turn right and so on. You want to create a smart car simulator that will drive users through their favorite places using the shortest paths. Each method represents a gene that can be multiplied and given some input (like, information about the previous gene). The genetic algorithm will then randomly join some of those methods to create first individuals and continue in the standard evolutionary iterative way: evaluate, breeding/crossover and mutation. The best fit individual is thus a series of available method calls, the program itself. To find the best solution, the algorithm should be run more times (even in parallel) and individuals in the population should vary to avoid locally optimal solutions.

There is an evolutionary framework for Python called DEAP (Distributed Evolutionary Algorithms in Python), that we can now use to quickly demonstrate the idea of genetic programming. Let us imagine we have an instance of a class named car with specific attributes such as the weight, fuel consumption and other important parameters of the given car. Then we have the methods to go forward to the next conjunction, to continue forward, left, right and so on. Now, we need to register all these methods to the genetic algorithm to get the best possible sequence of method calls. In DEAP, the set where these methods can be registered is called PrimitiveSet:

The first parameter of the primitive set is its name, the second is the list of input types and the last one is the output type. You can use simple primitive sets with no type specification, but from my experience it is always better to have the input/output types specified, even though for our use case they are irrelevant, because the object car iself remembers its position. Next, we have to register each method to the primitive set in the following way:

You can add a primitive, if you expect some input, or a terminal, if no input and no output from the method is expected (the car remembers its position inside the object’s attributes). We will also need to add a terminal number or an ephemeral constant, if there are methods expecting an input such as the stop_for method. When we have the primitive set ready, we can continue with setting up the genetic algorithm itself. The algorithm needs to first know what we are looking for. Let us register the following variables in the creator singleton:

In our task, we want to minimize the time spent by driving the car, hence we are looking for individuals with “minimum fitness”. And the individuals are represented by the sequence of methods formed in a primitive tree, which is a standard for joining the “genes” in genetic programming. Next, let us define all the parameters for the genetic algorithms such as evaluation, selection, mutation and so on. We can achieve this by using the Toolbox object:

First we define the maximum size of the tree (stored in treeMaximumHeight variable), then the way how individuals and populations are created, the evaluation function, which should here return the time spent by driving the car and possibly do some other calculations and so on. The most interesting part is the selection, where we use the so-called tournament selection. Each tournament selects a random number of individuals from the population and assigns a probability to every individual based on its fitness. The probability specifies how probable it is for the individual to win the tournament. There can be more tournaments based on the requested population size. The tournament size parameter specifies how many individuals (not necessarily different ones) there will be in a tournament. The winners of the tournaments are suitable for reproduction.

The reproduction/mate/crossover method is the simple one point crossover described above, while the mutation is a simple move of method calls in our case. After all the parameters are defined, we can choose the initial population (the size is up to us, but it should be big enough to ensure enough variation) and run the simple evolutionary algorithm with a certain number of generations and probabilities of crossover and mutation:

The list of method calls can be obtained inside the evaluate function (and performed as a program by deap.gp.compile(individual, primitive_set) inside the evaluateCar function) from the individual variable. For more information and a complete example, please refer to the DEAP framework, where genetic programming is illustrated on the so-called “Artificial Ant Problem”, which is very similar to our smart car problem: https://deap.readthedocs.io/en/master/examples/gp_ant.html